1 引言
未来战争将以信息化特征为主，战场物资消耗猛增剧涨，军事物流保障的任务更加繁重、责任更加重大。信息化战场环境要求军事物流必须适时、适地、适量地为作战部队提供物资保障，这给军事物流保障的快速性、机动性和准确性等提出了更高要求。RFID(Radio Frequency Identification)是一种基于射频原理实现的非接触式自动识别技术，随着其技术可靠性和可用性的提高，已被逐渐应用于军事物流领域，它使军事物流信息能够准确、可靠、快速、高效的传输、采集、处理和交换。具体对于RFID读写器而言，快速准确的采集信息就要求读写器能在较短的时间读取较多的标签。
然而，读写器和每个标签通信都是通过共同的信道，当多个标签和读写器通信时，传输的信号必然会发生冲突，这将使得读写器无法读出标签[1]。通常地，解决这类问题是采用防冲突算法，目前的防冲突的RFID标签算法按照系统模型种类可以分为两大类：随机型的和确定型的算法[2]。ALOHA类算法是随机型算法中最主要的一类算法，它基于概率论和时分多址的原理，将多个标签的信号在多个时隙内发送[3]。但是，当标签数量增多时，某些标签会在很长时间内也无法被读出，出现了标签漏读现象。确定型算法中有代表性的是二进制树[4]和询问树算法[5]。其中二进制树算法最早由Capetanakis[6]提出，用来解决随机多址问题，后来由Hush和Wood[4]将其有效地运用于RFID标签防冲突。二进制树算法把所有发生冲突的标签随机地分解为两个子集，一个子集为发送，另一个子集为等待，反复分解直到读到所有标签。虽然二进制树形算法读取标签的时间会有所增加，但是它基于分裂的原理，可以有效解决标签漏读问题，特别当标签数量增多时。
本文从减少标签读取时间出发，在二进制树算法的基础上，提出一种具有自动优先级分配的标签防冲突算法。该算法与传统二进制树形算法所不同的是，它可以自动地为发生冲突的每个标签分配一个优先级，而所有被分配优先级的标签将在时间上依顺序与读写器通信。因此，本算法可以有效地避免标签的冲突和空闲次数，从而减少了标签读取时间。从理论证明及仿真结果来看，本文提出的防冲突算法的读取时间要少于于传统的二进制树形算法。本文的剩余部分安排如下，第二部分介绍具有自动优先级分配的防冲突算法，第三部分对该算法的性能进行分析，第四部分分析仿真结果，最后一部分给出结论。
2自动优先级分配的RFID标签防冲突算法
2.1 系统定义
在本文中，系统由读写器和若干个标签构成，首先读写器发出命令，标签接收到命令后发送数据，若读写器成功接收到标签发送的数据，则读取标签信息结束。
一个读周期由三个阶段构成
1) 初始阶段，该阶段，读写器发出查询命令，在读写器覆盖范围内，所有接收到命令的标签准备发送数据。
2) 数据发送阶段，在该阶段，接收到查询命令的标签将发送数据，发送数据的顺序依初始的优先级号而定，若发生冲突，则执行自动优先级分配的算法，重新分配数据发送顺序。
3) 结束阶段，所有标签的数据均已发送完毕，一个读周期结束。
标签从开始发送数据到结束，定义为一个时隙，用
表示。根据每个时隙内标签数据发送的状态，将每个时隙定义为以下三种类型
1） 空时隙 在该时隙内没有数据发送，用
表示
2） 可读时隙 在该时隙内有且仅有一个标签数据发送，用
表示
3） 冲突时隙 在该时隙内有二个以上的标签数据进行发送，用
表示
在该算法中，规定四种数字号
1)
优先级号，每个标签都拥有一个并不唯一的优先级号，初始优先级号为一个随机整数，该优先级规定了标签在一个读周期内何时发送数据，优先级越大表明在越靠后的时隙内发送数据。优先级号用
表示。
2)
指针号，指针号随着成功发送数据的标签数目变化而变化，在每个读周期的初始时，指针号均为0，以后每成功发送一个标签数据，顺序加1。指针号用
表示。
3)
3) 
号，每个标签都拥有一个唯一的号，该号代表了每个标签的身份，该号在读周期的任何时候都不发生改变，标签向读写器发送的数据就是号。
4)
结束标识号，只要指针号超过结束标识号，那么就表明所有标签均已被读取完毕，一个读写周期结束。结束标识号用
。
根据每个标签是否发送数据的状态，将每个标签定义为以下三种状态
1)
激活，当某个标签的优先级号等于指针号时，该标签处于激活状态，在该状态下，标签可以发送数据，用
表示
2)
等待，当某个标签的优先级号小于指针号时，该标签处于等待被激活状态，在该状态下，标签不发送数据，用
表示。
3)
休眠，当某个标签的优先级号大于指针号时，该标签处于休眠状态，该状态表明该标签已发送过数据，直到下个读周期来临都不再发送数据，用
表示。
以上的系统各参数的表示符及含义见表1
表1 系统参数的表示符及含义
|
系统参数 |
表示符 |
含义 |
|
时隙 |
|
标签从发送数据到结束的时间 |
|
空时隙 |
|
时隙内无数据发送 |
|
可读时隙 |
|
时隙内仅有一个数据发送 |
|
冲突时隙 |
|
时隙内有二个以上的数据同时发送 |
|
标签数 |
|
读写器范围内所有标签的总数 |
|
优先级号 |
|
规定在一个读周期内何时发送数据 |
|
指针号 |
|
成功发送标签的数目 |
|
标签身份号 |
|
代表标签身份 |
|
激活状态 |
|
该状态下，标签可以发送数据 |
|
等待状态 |
|
该状态下，标签等待被激活 |
|
休眠 |
|
该状态下，标签已发送过数据 |
2.2 算法步骤
1初始时，系统的为0，所有标签的为
的一个随机数，读写器发出查询命令，所有接收到命令的标签在下一个时隙开始时执行相应的操作。
2时隙开始时，若>，则转为7，否则转为3。
3所有小于系统的标签处于状态，所有大于的标签处于状态W，所有等于的标签处于状态。若只有一个标签的等于系统，转到4；若没有任何标签的等于系统，转到5；若有两个以上标签的等于系统的，转到6
4此时为时隙，标签被成功读取，自动加1。转回2
5 此时为时隙，没有标签成功发送，所有处于W标签的自动减1。转回3
6此时为时隙，没有标签成功发送。所有处于状态A的标签被随机分为两个子集，其中一个子集的标签加0，另一个子集的标签加1；另外，所有处于标签的也加1。下一个时隙开始时，转回3
7一个读周期结束
从以上的算法步骤可以看出，读写器根据标签的PN大小来先后读取标签的，由于标签的初始是随机分配，因此它可以大大减少标签冲突的次数。如果出现标签的相同的情况，可以采用步骤6的方式，重新对标签的进行分配。
2.3 算法举例
在首个读周期内，标签的初始号被随机分配，读写器将根据标签的号的大小顺序依次读取标签信息，若标签出现相同的，则执行相应的冲突分解。在这种情况下，读取标签的时间将与标签的冲突时隙数密切相关，而冲突时隙数又与标签的初始分配情况相关。图1给出了三个标签在首个读周期内被读取的示例图，图中节点旁标出了标签的和当前时隙的，被标出的标签表示在当前时隙下为状态，每个节点分支旁所标的数字-1，0，1表示了，应给标签的所加的数字，横坐标表示了系统和的变化。在图1(a)中我们看到，由于三个标签的相同，因此冲突时隙相应增多，整个读取过程需要6个时隙，实际上这就退化为传统的二进制树冲突算法。图1(b)给出了较为理想的情况，三个标签的初始号均不相同。在这种情况下，不存在时隙，只有时隙，相对(a)总的时隙较少。
从图1中我们可以看出，经过首个读周期后，在读写器所覆盖的所有标签均被自动分配了唯一的，且这些按
依次排列。因此，在第
次读周期时，若无标签离开或到来，将不存在和时隙；若有标签离开，将只有时隙；若有标签到来，将只与其相同的标签发生冲突。图2给出了三个标签在第
次读周期内，无标签变化及其有标签变化时的情况。
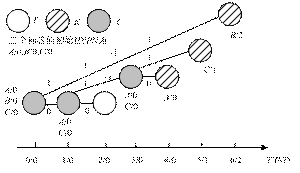
(a)标签PN均相同
(b)标签PN均不同
图1 首个读周期的算法执行示例图
(a)
(b)
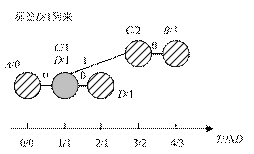
(c)
(d)
图2 非首个读周期算法执行示例图
4 性能分析
引理1 采用二进制树形冲突算法读取
个标签的平均时隙数为
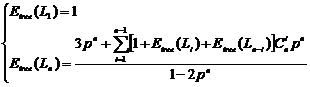（1）
其中，
数学期望，
成功读取个标签需要的时隙数，
在个元素中取个元素的排列数，
将所有发生冲突的标签分为发送和等待的概率，在二进制树形算法中，发送和等待的概率相同，且均为1/2。
证明：只有一个标签时，不会发生冲突，因此有
。
当>1时，可分为三种情况，
1发送数据的标签数为0，等待标签数为，此时的概率为
，所需时隙数为
2发送数据的标签数为，等待标签数为0，此时的概率为
，所需时隙数为
3发送数据的标签数
等待标签数为
，此时的概率为
，所需时隙数为
，因此，我们有
移项，合并后得证。
3.1首个读周期
定理1 若个标签的初始优先级号随机分配为0-的整数，则采用自动优先级分配算法，在首个读周期内成功读取个标签所需的平均时隙数为
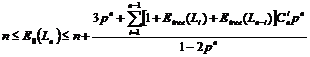（2）
证明：成功读取个标签所需的平均时隙数主要与标签所分配的初始优先级号有关，可以从以下两种情况分析：
1当个标签的初始优先级号均不重复地分配为0-时，所需的时隙数最少，此时
2当个标签的初始优先级号均为时，所需的时隙数最多，此时的时隙数应为个时隙和采用二进制树形算法读取个标签所需时隙之和，因此
。
根据以上两种情况，并根据（1）式，（2）式得证。
3.2非首个读周期
定理2自动优先级分配算法在第
个读周期内，成功读取个标签所需的平均时隙数为
(3)
证明：根据2.2的算法步骤，可知，个标签在首个读周期内被成功读取后，其优先级将自动分配为
，因此在第
次读取标签时，优先级分别为的标签将依次传送数据，此时所需的时隙共为个。
定理3在第
个读周期开始时，原个标签中有
个标签离开，采用自动优先级分配算法读取所有标签的平均时隙数
(4)
证明：当有个标签离开时，在
个读周期内将留下个E时隙，而读取
个标签还需要个时隙，所以总共需要
个时隙，得证。
定理4在第个读周期开始时，原个标签中有
个标签到来，采用自动优先级分配算法读取所有标签的平均时隙数满足
(5)
证明：当有个标签到来时，所需的时隙数最多的情况是，个标签的优先级与个标签中的一个相同，此时所需的时隙数为
，得证。
定理5在第个读周期开始时，原个标签中有个标签离开个标签到来，采用自动优先级分配算法读取所有标签的平均时隙数满足
(6)
证明：由(4)和(5)得证。
3.3与二进制树形算法的比较
定理6 当标签数足够大时，采用自动优先级分配算法成功读取标签所需平均时隙数不会多于二进制树形算法
证明：可以分为二种情况来证明，分别是
1标签无移动
由式(2)可知，在第0个周期采用自动优先级分配算法成功读取标签所需的平均时隙数满足
。当较大时，我们有
，此时有
和
，因此
(7-a)
由(2)可知，在第个周期采用自动优先级分配算法成功读取标签所需的平均时隙数满足
，再由(7-a)可得
，因此
(7-b)
2标签有移动
设在第个读周期开始时，原个标签有个标签离开个标签到来。因为
足够大，所以
，又因为
，可以得到
。根据定理5，可以得到
(7-c)
综合(7-a)-(7-c)，得证。
4 仿真结果分析
本节我们采用仿真试验，将本文的算法与二进制树形算法做对比，分析两种算法在一个读周期内读取所有标签所需的时隙数。试验采用Monte-Karlo方法，所有结果由独立地做50次试验取平均得到。在自动优先级分配的算法中，假定标签数目均为已知，为标签数目，当超过时，一个读周期结束。另外，标签的初始为0-的随机整数，下面我们分别从两个方面分析试验结果。
4.1标签无移动
标签无移动指的是，没有新的标签到来，也无标签离开。图3给出了标签无移动时，时隙数随标签数变化的情况的算法对比。从图中可以看到，在首个读周期内，自动优先级分配的时隙数要少于二进制数算法，特别地，当随着标签数目增大，与二进制数算法相比，所需的时隙数更少。其原因是，在自动优先级分配算法中，每个标签均被分配了一个初始号，虽然有号相同的情况，但是，与二进制树形算法相比，冲突时隙数有所减少。在非首个读周期内，与二进制数算法相比，自动优先级分配所需的时隙数进一步减少，这是因为，在经过首个读周期内，标签的将自动分配为0,1,2,…的整数，在之后的周期内只需要个周期。
4.2标签有移动
标签有移动的情况也从三个方面分析，分别是有标签离开，有标签到来和同时有标签离开到来，其中有离开和到来的标签的都是随机的，并且均假定原标签数目
=300。
图4给出了所需时隙数随离去标签变化的算法对比结果，从图中可以看到，当离去的标签数有所变化时，自动优先级分配所需的时隙数变化并不大，这是因为，当有标签离去时会留下很多空时隙。而对于二进制树算法，当标签离去，总的标签数减少，所需的时隙数也自然减少。从图中还可以看到当标签离开的数目大于60%左右时，二进制树形算法所需时隙数将开始少于自动优先级分配。
图5给出了有新的标签到来时所需时隙数的变化情况。在这种情况下，自动优先级分配的时隙数明显少于二进制树形算法。在自动优先级分配算法中，原来的标签经过首次读周期后，已被自动分配，当有标签到来时，冲突时隙只发生在当新来的标签与原来标签相同时，因此相对于二进制树形算法，总的时隙数较小。
图6给出了，同时有标签离开和到来时，所需时隙数的变化情况。在这里，我们假定标签离开数和标签到来数相同，即总的标签数不变。由于总的标签数不变，因此二进制树算法所需的时隙数也不变。而对于自动优先级分配算法，随着离开和到来标签数的增多，时隙和时隙将有所增加，因此所需时隙数也将增加，但不会超过二进制树形算法。
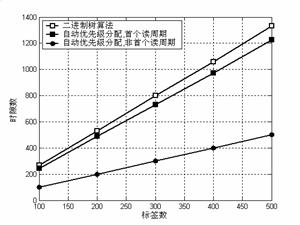
图3 无标签移动时算法对比
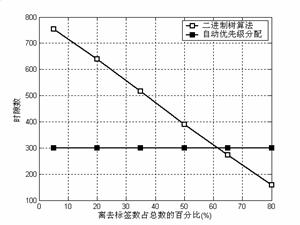
图4 有标签离去时的算法对比
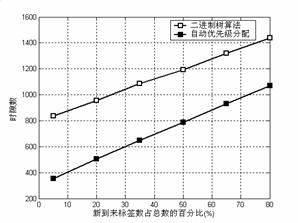
图5 有标签到来时的算法对比
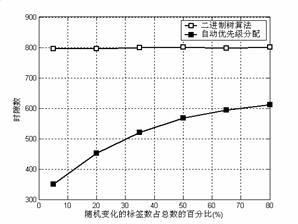
图6 同时有标签到来和离去时的算法对比
6 结论
在自动优先级分配算法中，每个标签被初始分配一个号，经过一次读周期后，所有标签的将被依次分配为0,1,…，因此之后的周期，所需时隙数只需个。从理论上证明，当标签数足够大时，自动优先级分配算法所需的时隙数不会多于二进制树形算法。从仿真结果中，我们可以得到，当标签数无变化时，与二进制树算法相比，自动优先级分配算法在首个读周期和非首个读周期内，所需的时隙数都较小；当有标签离开时，二进制数算法所需的时隙数变化不大，同时，若离去标签数不多，所需时隙数仍少于二进制数算法；当有标签到来时，自动优先级分配算法所需时隙数明显少于二进制树算法；当同时有标签离开和到来时，自动优先级分配算法所需时隙数，随变化标签的数目增多而增多，但仍不会超过二进制树形算法。
参考文献：
1 K. Finkenzeller, RFID
Handbook: Radio-Frequncy Indetification Fundamentals and Applications in
Contactless Smart Cards and Identification, Second Edition, Jhon Wiley,
2 D.H. Shih, P. L. Sun, D. C. Yen,
S.M. Huang, Taxonomy and survey of RFID anti-collision protocols, ELSEVIER, Computer
communications,2006, Vol.29,. No.11, pp.2150-2166
3 Vogt H.
Multiple object identification with passive RFID tags. IEEE International
Conference on Systems, Man and. Cybernetics, Vol. 3, October 2002.
4 D. R. Hush
and C. Wood, Analysis of tree algorithm for RFID arbitration, Proc. of IEEE International Symposium on
Information Theory, pp. 107, 1998.
6
Capetanakis, J. I. Tree Algorithms for Packet. Broadcast Channels. IEEE
Transactions on. Information Theory, vol. IT-25, no. 5, Sept. 1979, pp.
505–515.
作者简介：
吴海锋，男，1977年生，2007年进入昆明船舶设备集团有限公司与中山大学联合培
单位：云南昆船设计研究院
地址：昆明市人民中路6号
邮编：650051
电话：13668706480，0871-8326193
Email：wuhaifeng@mail.ksec.cn.